Fyzika – obsah > Mechanika – teorie srozumitelně > Rovnoměrný pohyb po kružnici — úhlová a obvodová rychlost
Rovnoměrný pohyb po kružnici — úhlová a obvodová rychlost
Rovnoměrný = nemění se velikost rychlostí.
U rovnoměrného pohybu pro kružnici máme totiž dvě rychlosti – úhlovou a obvodovou.
Směr úhlové rychlosti se zachovává, směr obvodové rychlosti se mění (viz dále).
Po kružnici – bod na plášti jedoucího kola, kabinka centrifugy, …
Rychlost obecně
Rychlost se u rovnoměrného pohybu obecně vypočítá jako

Změna dráhy dělená změnou času. Zkrátka o kolik se změní dráha (o kolik naroste) za určitou dobu.
Ten „trojúhelníček” je velké řecké písmenko delta. Říká nám, že se jedná o změnu (prostě, že se dráha a čas změnily z nějaké počáteční hodnoty na jinou). Za deltu nedosazujeme žádná čísla, ani není jaká. Ta nám jen říká, že došlo k nějaké změně v hodnotě dráhy a času.
Úhlová rychlost
U rovnoměrného pohybu po kružnici se zavádí tzv. úhlová rychlost.
Vše si ukážeme na následujícím obrázku.
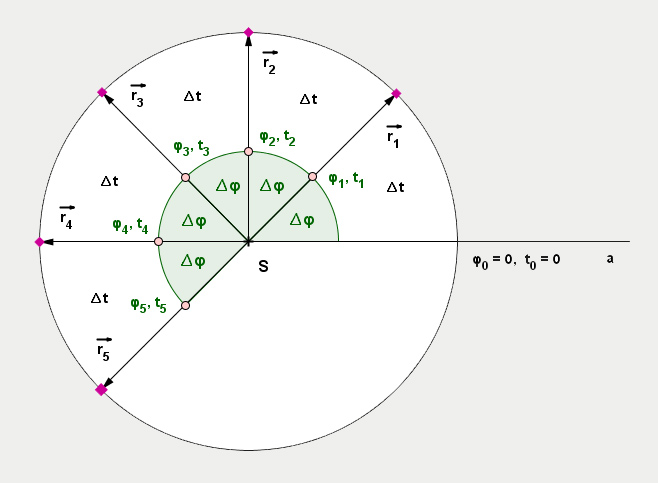
Polopřímka a … startovní čára, odtud začínáme měřit polohu a čas, bod se na kružnici otáčí doleva
Fialový kosočtverec na kružnici, vektory … poloha bodu v jednotlivých časech na kružnici; poloha je určena polohovými vektory (r1, r2, r3, r4, r5)
Vektorům se také říká průvodiče.
φ1, φ2, φ3, φ4, φ5 … úhly, které bod urazí (které opíše průvodič) za určitou dobu
Jejich velikosti měříme od startovní čáry (úhel φ2 je tedy větší než úhel φ1 atd.).
∆φ = φ1 − φ0 = φ2 − φ1 = φ3 − φ2 = φ4 − φ3 = φ5 − φ4
t1, t2 ,t3 ,t4 ,t5 … určitý čas naměřený od začátku pohybu bodu
Čas měříme od startovní čáry (čas t1 je tedy větší než čas t2 atd.).
∆t = t1 − t0 = t2 − t1 = t3 − t2 = t4 − t3 = t5 − t4
∆φ … úhel, který bod urazí za dobu ∆t
Při rovnoměrném pohybu bod urazí (průvodič opíše) za stejnou dobu ∆t stejně velký úhel ∆φ. Úhlová rychlost nám pak říká, jak velký úhel bod na kružnici opsal za určitou dobu.

Obvodová rychlost
nám říká, jak velký oblouk na kružnici bod urazí za určitou dobu. Více zase na následujícím obrázku.
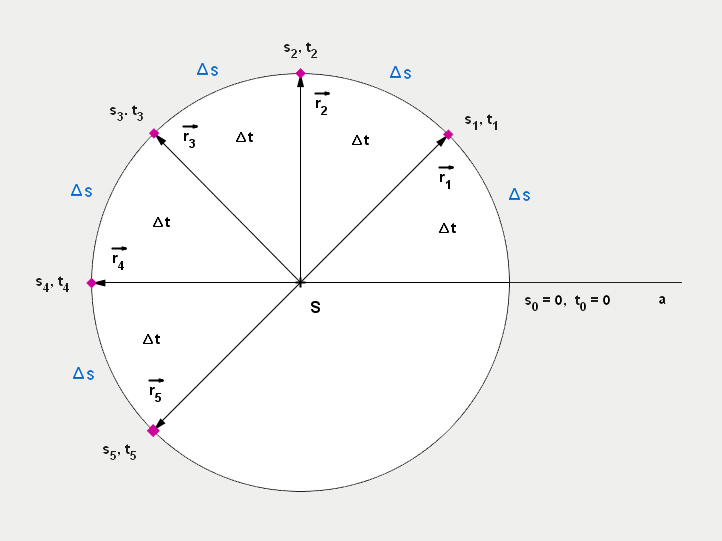
Vztah pro výpočet obvodové rychlosti (prostě jak rychle lítá bod na té kružnici) je zřejmý:
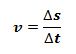
Při rovnoměrném pohybu bod za stejnou dobu ∆t urazí stejnou vzdálenost ∆s.
My si ukážeme, jak spolu souvisí úhlová a obvodová rychlost (chceme do jednoho vzorečku dostat obvodovou i úhlovou rychlost). Začneme opět obrázkem…

Obrázek k výkladu vztahu úhlové a obvodové rychlosti
Pozn.: Pokud měříme úhel a dráhu od počátku (startovní čáry), nemusíme psát u písmenek deltu. Delta dané veličiny se totiž vypočítá jako koncová hodnota mínus hodnota počáteční. Na startovní čáře jsou počáteční hodnoty nulové, takže nám ve výpočtu zbude pouze hodnota koncová.
Můžeme si to představit jako dvojitý kolotoč, který se otáčí kolem středu S, a na jednom rameni mohou sedět dva lidé. V našem případě Jiříček (označený písmenem J) a Pavlínka (označena písmenem P).
Z počáteční polohy (ze startovní čáry) se za určitou dobu oba posunuli do polohy nové. Průvodič (v našem případě rameno kolotoče), na kterém sedí, opsal úhel φ. Oba tedy od počáteční polohy urazili stejný úhel. Pavlínka, která je dále od středu, však urazila větší dráhu. Jelikož za stejnou dobu urazila větší dráhu, svištěla si to na kolotoči větší rychlostí.
Z obrázku je patrné, že úhlová rychlost je pro oba stejná. Pavlínka i Jiřík urazí za stejnou dobu stejný úhel. Obvodová rychlost je však rozdílná. Čím dále od středu (větší poloměr) tím je rychlost vyšší, jelikož je třeba urazit větší dráhu. Obvodová rychlost tedy bude záviset na poloměru, a to přímo úměrně (čím větší poloměr, tím větší dráha, a tím vyšší rychlost).
Vztah mezi úhlovou a obvodovou rychlostí již není těžké uhodnout. My si ho však odvodíme.
Připomene si definici radiánu (a opět pomocí obrázku):
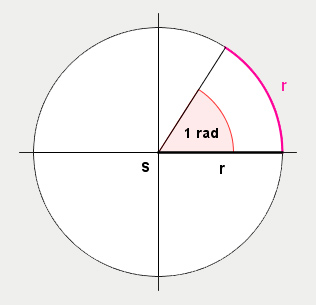
Otázka zní:
Jak vypočítáme, kolik radiánů se vejde do oblouku, pokud známe délku oblouku a poloměr?
Když se podíváme na obrázek, tak délka oblouku je r, poloměr má délku také r, a máme dostat jedničku (1 radián). Nabízí se, že vydělíme „jedno erko druhým erkem”. Ale které budeme dělit kterým? Zkusíme tedy ještě jeden příklad.
Víme, že celý oblouk kružnice má 2π rad. Délka oblouku (délka kružnice) je 2π ∙ r. Poloměr je r. Platí tedy:

Abychom dostali počet radiánů v oblouku, musíme vydělit délku oblouku poloměrem.
Obecně tedy platí:

Pro naši kružnici (dvojitý kolotoč) platí:
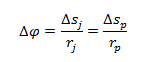
Pak

Pro obvodové rychlosti Pavlínky a Jiříka můžeme psát:

Nyní přijde hlavní krok odvození vztahu mezi úhlovou a obvodovou rychlostí.
Dosadíme do vztahů pro obvodovou rychlost za ∆sp a ∆sj z výrazů v rámečku.

Výrazy ještě trochu upravíme:
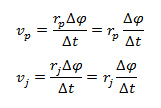
Vysunuli jsme poloměry před zlomek. Nyní je krásně vidět, že zlomek ve výrazech něco představuje (dá se za něj něco dosadit).

Obecně tedy můžeme psát:
v = ω ∙ r
Obvodová rychlost bodu je při dané úhlové rychlosti tím větší, čím dále od osy otáčení se bod nachází.
Směr úhlové a obvodové rychlosti
Směr úhlové rychlosti určíme podle pravidla pravé ruky. Skrčené prsty ukazují směr otáčení a vztyčený palec ukazuje směr úhlové rychlosti. Počátek vektoru umísťuje do středu kružnice.

Vektor úhlové rychlosti
Zkuste si na tento obrázek „napasovat” pravou ruku podle řečeného pravidla.
Proč je vektor úhlové rychlosti právě takhle, má trochu složitější vysvětlení. My se zatím budeme zabývat pouze velikostí úhlové rychlosti.
Směr obvodové rychlosti je vždy tečnou ke kružnici (kolmicí k poloměru) v daném bodě. Vektory okamžité obvodové rychlosti ukazují, jakým směrem by předmět letěl, pokud by se v daném místě z kružnice uvolnil. Vektory (šipky) jsou stejně dlouhé, jelikož velikost obvodové rychlosti je pořád stejná (rovnoměrný pohyb), směr se však mění.

Vektory okamžité obvodové rychlosti, pokud se bod na kružnici otáčí doleva
Stáhnout jako PDF [204 kB]