∇ nabla – fyzika

Fyzika – obsah > Mechanika – teorie srozumitelně > Rovnoměrně zrychlený přímočarý pohyb

Rovnoměrně zrychlený přímočarý pohyb

Rovnoměrně zrychlený = zrychlení je stále stejné = velikost rychlosti se každou sekundu zvýší (případně sníží) o stejný díl

Rychlost

v = a ∙ t

v … okamžitá rychlost
a … zrychlení, se kterým se dané těleso pohybuje
t … určitá doba (prostě doba jízdy, běhu, …)

Výše uvedený vztah nám říká, že rychlost se každou sekundou mění o stejný díl.
Jak je ten díl velký, nám prozrazuje veličina zvaná zrychlení → a (vizte dále).

Pokud se těleso už nějakou rychlostí pohybovalo („nezrychlovalo z nuly”) platí:
v = v₀ + a ∙ t
v₀ … počáteční rychlost

Pokud „zrychluje z 0”, v₀ = 0 a dostáváme v = a ∙ t.
Vztah v = v₀ + a ∙ t je tedy obecnější.

Zrychlení

O zrychlení mluvíme vždy, když se mění vektor rychlosti. To znamená vždy, pokud se mění velikost rychlosti, směr rychlosti nebo obojí. U rovnoměrně zrychleného přímočarého pohybu se mění velikost rychlosti, směr ne – proto je ten pohyb přímočarý.

Zrychlení je vektor.

Velikost průměrného zrychlení u rovnoměrně zrychleného přímočarého pohybu za celkovou
(námi sledovanou) vypočítáme:

O kolik se změní rychlost za určitou dobu.

Ten trojúhelníček je velké řecké písmenko delta. Říká nám, že se jedná o změnu rychlosti (prostě, že se rychlost změnila z nějaké hodnoty na jinou). Δt pak říká, že se čas změnil z nějaké hodnoty na jinou. Za deltu nedosazujeme žádná čísla, ani není jaká. Ta nám jen říká, že došlo k nějaké změně v hodnotě rychlosti či času.

Na příkladě to snad dokážu vysvětlit lépe…

♦  Auto zrychlí z rychlosti 10 m ∙ s⁻¹ na rychlost 30 m ∙ s⁻¹ za 4 sekundy. Rychlost se tedy změnila o 20 m ∙ s⁻¹ za 4 sekundy.

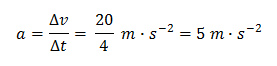
Zrychlení tedy říká, že se velikost rychlosti každou sekundu změní (vzroste) o 5 m ∙ s⁻¹.

U rovnoměrně zrychleného přímočarého pohybu je zrychlení konstantní.
(Stejně tak, jako rychlost u rovnoměrného přímočarého pohybu.)

Dráha

Pokud si řekneme, že dráha se vlastně vypočítá jako průměrná rychlost krát doba, máme vyhráno. Teda zatím jen napůl, ale jsme na dobré cestě.

s = v_p ∙ t

Mírný problémem je to, že rychlost není stálá, ale rovnoměrně se mění. Průměrnou rychlost tedy budeme muset nejdříve vypočítat.

Vyjdeme z předchozího příkladu. Jelikož se rychlost zvyšuje z 0 m ∙ s⁻¹ na 20 m ∙ s⁻¹ rovnoměrně, průměrná rychlost se vypočítá jako aritmetický průměr těchto dvou rychlostí.

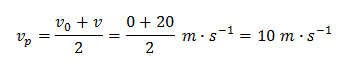
Pro dráhu tedy platí (dosadíme za v_p):

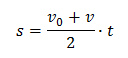
Za v dosadíme ze vztahu v = v₀ + a ∙ t

A upravíme:

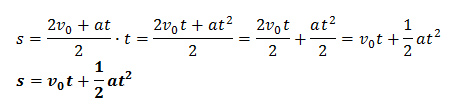
Pokud je počáteční rychlost nulová (třeba auto se rozjíždí z klidu), první člen vypadne a my dostaneme:

Shrnutí

rychlost	dráha
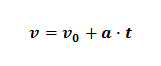S nulovou počáteční rychlostí	S nulovou počáteční rychlostí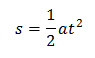

Pokud auto brzdí, taky zrychluje (lidově říkáme, že zpomaluje). Pohybuje se vlastně se záporným zrychlením (vektor zrychlení má opačný směr, než vektor rychlosti).

Velikost zrychlení nám v tomto případě udává, o jak velký díl svou rychlost každou sekundu zmenší.

♦  Auto sníží svoji rychlost z 30 m ∙ s⁻¹ na 10 m ∙ s⁻¹ za 4 sekundy. Rychlost se tedy změnila o 20 m ∙ s⁻¹ za 4 sekundy.

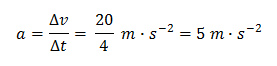
Zrychlení tedy říká, že se velikost rychlosti každou sekundu změnila (snížila se) o 5 m ∙ s⁻¹.

Tabulka pak vypadá následovně:

rychlost	dráha
S nulovou počáteční rychlostí Počáteční rychlost nemůže být nulová. Aby totiž těleso mohlo svoji rychlost snižovat, musí se nejdříve nějakou nenulovou rychlostí pohybovat.	S nulovou počáteční rychlostí Počáteční rychlost nemůže být nulová. Aby totiž těleso mohlo svoji rychlost snižovat, musí se nejdříve nějakou nenulovou rychlostí pohybovat.

Grafy

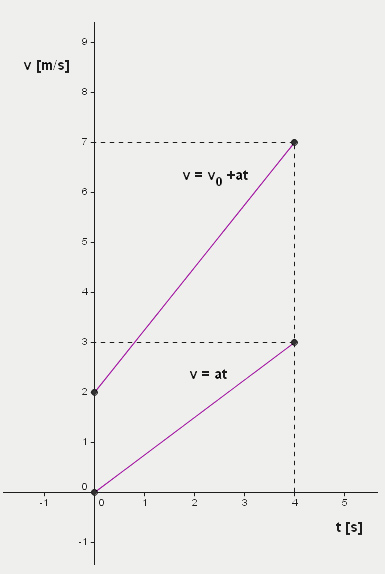
Graf závislosti rychlosti na čase rovnoměrně zrychleného pohybu s kladným zrychlením

Křivka popsaná jako v = v₀ + at nám říká, že se těleso v počátku našeho měření již pohybovalo nějakou nenulovou (počáteční) rychlostí v₀. V grafu má hodnotu 2 m ∙ s⁻¹.

Velikost průměrného (i okamžitého) zrychlení první křivky (s nulovou počáteční rychlostí v₀₀) je:

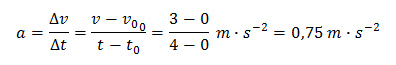
Rychlost každou sekundou narostla o 0,75 m ∙ s⁻¹

Druhá křivka:

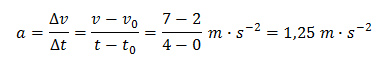
Rychlost každou sekundou narostla o 1,25 m ∙ s⁻¹

Zrychlení u druhé křivky je tedy větší, což je vidět na první pohled, protože křivka je strmější.

Graf pro dráhu objasníme na příkladu.

♦  Auto zrychlí rovnoměrně zrychleným pohybem z 0 km ∙ h⁻¹ na 72 km ∙ h⁻¹ za 10 sekund.

Auto se rozjíždí z klidu, pro dráhu tedy platí:

Nejprve si průběh dráhy v čase napíšeme do tabulky a poté vyneseme do grafu.

Do tabulky k jednotlivým časům budeme doplňovat příslušnou dráhu, podle předchozího vztahu. Neznáme však velikost zrychlení. Jelikož ale známe, velikost celkové změny rychlosti za dobu 10 sekund, velikost zrychlení snadno vypočítáme (dosazovat budeme v základních jednotkách).

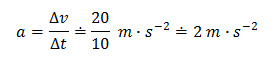
t [s]	0	1	2	3	4	5	6	7	8	9	10
s [m]	0	1	4	9	16	25	36	49	64	81	100

Tabulku teď převedeme na graf:

Graf závislosti dráhy na čase rovnoměrně zrychleného pohybu s kladným zrychlením

A jak budou vypadat grafy pro rychlost a dráhu rovnoměrně zrychleného pohybu se záporným zrychlením (rovnoměrně „zpomaleného” pohybu)?

Učebnici fyziky s tématem rovnoměrného zrychleného pohybu pro základní školy najdete v eshopu UcebniceMapy.cz

A najdete ta i učebnice mechaniky pro gymnázia. Obě jsou z nakladatelství Prometheus

Stáhnout jako PDF  [197 kB]