∇ nabla – fyzika

Fyzika – obsah > Mechanika – teorie srozumitelně > Hybnost, impuls síly

Hybnost, impuls síly

Představme si letící tenisový míček a medicinbal. Oba letí rychlostí 30 km ∙ h⁻¹. Tenisák má hmotnost 58 gramů a medicinbal 3 kilogramy.

Žákyň a žáků se ptám, co nám dá větší námahu, jestli zastavit tenisový míček nebo medicinbal.

Občas se sice objeví provokatér, který bude tvrdit, že pro něj by byla menší námaha zastavit medicinbal, ale většina se shodne, že větší námahu musíme vynaložit na zastavení medicinbalu.
Úsilí, které musíme vynaložit na zastavení míče, tak určitě závisí jeho hmotnosti. Závisí ale také na jeho rychlosti; určitě bude náročnější míče zastavit, kdyby letěly vyšší rychlostí.

Veličina, která udává, „jak moc” se tělesa pohybují, se nazývá hybnost. Je to vektorová veličina.

p = mv
[p] = kg ∙ m ∙ s⁻¹

Příklad:
Jakou rychlostí by musela letět moucha o hmotnosti 0,2 g, aby měla stejnou hybnost jako vlak o hmotnosti 2500 t, který jede rychlostí 30 km ∙ h⁻¹?

Výsledek příkladu evidentně nebude reálný. Procvičí nás však v počítání s mocninami.

Hybnost vlaku
p_v = m_vv_v

Hybnost mouchy
p_m = m_mv_m

Hybnost mouchy se má rovnat hybnosti vlaku:
p_m = p_v
m_mv_m = m_vv_v

Z této rovnice si vyjádříme rychlost mouchy a dosadíme čísla.

(1,350 biliónů metrů za sekundu; pro představu přibližně 33750krát kolem Země za sekundu)

Výsledek je nejen nereálný, ale fyzikálně nesmyslný. Moucha by totiž musela letět mnohem rychleji, než je rychlost světla (3 ∙ 10⁸ m ∙ s⁻¹).

Druhý Newtonův pohybový zákon zapsaný pomocí hybnosti

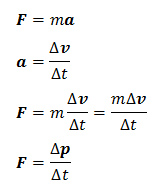
Působící síla se rovná změně hybnosti za dobu.

Impuls síly

F∆t = ∆p

Součinu síly a doby na levé straně rovnice se říká impuls síly. Je roven změně hybnosti za tuto dobu.

Objasníme si to na pokusu…

Mějme nějaký předmět zavěšený na niti; na jeho spodní straně budou přivázány další dvě nitě.

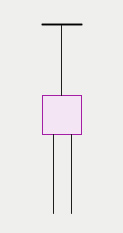
Pokud první nití silně škubneme, budeme sice na těleso působit silou, ale doba působení této síly bude krátká (∆t malé). A pokud síla škubnutí nebude příliš velká, bude i změna hybnosti malá a těleso se udrží pověšené na niti a my nejspíš přetrhneme nit, za kterou taháme.

Pokud budeme za druhou nit tahat pomalu (dlouho) určitou silou, bude doba působení této síly dlouhá (∆t velké) a tím bude velká i změna hybnosti (∆p). Hybnost tělesa se tedy dostatečně změní – těleso se utrhne z nitě, na které je zavěšeno. Samozřejmě, že také záleží na velikosti síly, kterou táhneme.

Stáhnout jako PDF  [131 kB]