Matematika – úvod > Maturita z matematiky > Soubor řešených vzorových úloh > Číselné obory
Mezi 0 a 2/3 je 8 dílků. Jeden dílek tedy je 2/3 : 8 = 2/24 = 1/12.
1/2 = 6/12, od nuly se tedy posuneme o 6 dílků.
5/6 = 10/12, od nuly se tedy posuneme o 10 dílků.

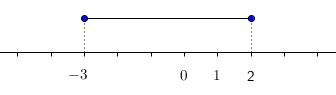
Dosadíme do intervalu za n. Dostaneme interval <-3; 2>
Je to uzavřený interval, čísla -3 a 2 do něj patří. Body (kolečka) musí být nakresleny vyplněné.
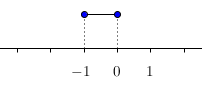
Přirozené číslo je kladné celé číslo. Pokud dosadíme 1 nebo 2, interval nebude dávat smysl. Pro číslo 3 pak už dostaneme smysluplný interval <-1; 0>. Ten zobrazíme na číselné ose.

Číslo 1017 je větší než součet čísel 3,2 ∙ 1015 a 8 ∙ 1014 25krát.
Podle obrázku 15 cm na mapě odpovídá 7,5 km ve skutečnosti. Tedy:
15 cm odpovídá 7500 m
15 cm odpovídá 750 000 cm
1 cm odpovídá 50 000 cm.
Měřítko mapy je 1 : 50 000.
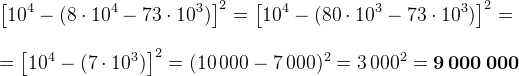
1 % ze 2 miliard je 20 milionů.
5 setin z 20 milionů je 20 milionů : 100 ∙ 5 = 200 000 ∙ 5 = 1 000 000.
5 setin procenta ze 2 miliard korun je 1 000 000 korun.
(1/2 - 1/3) nádrže odpovídá 100 km a (1/3 - 1/5) nádrže odpovídá zbytku vzdálenosti.
1/6 nádrže odpovídá 100 km a 2/15 nádrže odpovídají zbytku.
Patnáctina je 2,5krát mennší než šestina (15 : 6). Jedné patnáctině tedy odpovídá 100 : 6 kilometrů. Dvěma patnáctinám
pak 100 : 6 ∙ 2 kilometrů = 80 kilometrů.
Auto ujelo (100 + 80) km = 180 kilometrů.