Matematika – úvod > Maturita z matematiky > Řešené maturitní testy > Ilustrační test 2013 — řešení


Vysvětlíme si to ještě na penězích. Já mám 100 Kč a můj kamarád má 80 Kč. On má tedy o 20 % méně, než já. Já však mám 125 % jeho jmění, mám tedy o 25 % peněz více. K výsledku jsme se dostali tak, že jsme 100 vydělili jedním procentem z 80.
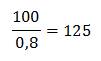

Činí Vám tento příklad problémy? Zopakujte si počítání s mocninami.

Zde si je potřeba pouze uvědomit, co znamená otevřený a uzavřený interval.








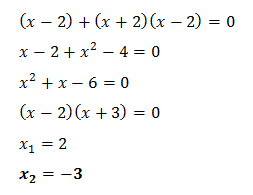
Podívejte se, jak počítat s kvadratickými rovnicemi.

8.1
Hledáme souřadnice bodů B a D, které leží na úhlopříčce f.
B (b1; b2) D (d1; d2)
Jelikož se úhlopříčky rovnoběžníku vzájemně půlí, body B a d jsou středově souměrné podle bodu S (4; 4) – vyčteno z obrázku.
Napíšeme podmínky (rovnice), které platí pro souřadnice bodů, a vyřešíme soustavu rovnic:


8.2
Délku uhlopříčky vypočítáme pomocí Pythagorovy věty
(viz vyznačený pravoúhlý trojúhelník na předchozím obrázku).

9.1
Jedna sekunda trvá nkrát méně než n sekund (n : n = 1). Za jednu sekundu se tedy vytiskne

9.2
n minut je 60krát více než n sekund. Pokud se za n sekund vytiskne 20 listů, za n minut se vytiskne
20 ∙ 60 listů = 1200 listů.


Ve výpočtu jsme využili pravidla, že rozdíl logaritmů se rovná logaritmu podílu.



Máme určit, kolik je 40 % z 360 °.
10 % odpovídá 36 °, 40 % je 4krát více, tedy 36 ° · 4 = 144 °.

Obsah pláště (obdélník) si označíme Q, výšku pláště h. Délku pláště pak spočítáme jako obvod kruhu (podstavy válce).


Na první pohled je vidět, že obsah pláště se snížil o 4 %.

Přirozené číslo je kladné a celé (1, 2, 3, 4, 5, …). Podle zadání platí:

Pozor. Pokud bych v první rovnici použil 0,5c, musel bych ve druhé rovnici použít 0,75c, nikoli 1c. Rozdíl by totiž nebyl 50 %, ale 100 %.
Máme tedy soustavu dvou rovnic. V první rovnici máme už vyjádřené c, dosadíme tedy za c do rovnice druhé
a pak podle zadání dosadíme za b číslo 15.
Proč tu patnáctku dosadíme za a a ne za b?
Rozdíl by totiž vyšel záporný (15 je podle zadání menší číslo);
a jelikož součet dvou přirozených čísel je vždy kladný, neplatila by podmínka ze zadání, že součet je větší o 50 %.




16.1
Podle tabulky si dvakrát zapomnělo úkol 6 žáků. 6 z 20 (celkový počet žáků) je 30 %.
První odpověď je tedy ANO.
16.2

Odpověď je NE.
16.3
Modus je hodnota, která se vyskytuje nejčastěji. Podle tabulky je nejčastěji vyskytující se hodnotou 3 (8krát).
Odpověď je tedy NE.
16.4
Medián je hodnota, která se nachází uprostřed souboru čísel seřazených podle velikosti.
V našem případě je tou hodnout 2.
Odpověď je ANO.

Jedná se o vyjádření neznámé (v našem případě s) ze vzorce.

Správná odpověď je tedy C.
Váhali jste? Zopakujte si vyjadřování neznámé ze vzorce.

4 osoby složí 240 beden → jedna osoba tak složí průměrně 60 beden
3 osoby složí 240 beden → jedna osoba tak složí průměrně 80 beden.
Podle zadání platí (počet hodin 4 osob jsme si označili H):

Správná odpověď je tak B.
Můžeme to napsat také následovně; tentokrát je však písmenem H označen počet hodin práce 3členné skupiny. Od výsledku tak musíme odečíst ještě 1 hodinu.
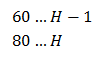

Vypočítáme, kolik peněz tam pan Novák měl po 6 letech. Pak odečteme počáteční vklad a tím zjistíme čistý zisk.

Správná odpověď je tedy C.

Jedná se o příklad na aritmetickou posloupnost.
Počet řad spočítáme jako počet trojúhelníku v dolní řadě + 1, to celé děleno 2. Tím zjistíme, kolik řad obsahuje trojúhelník s 31 trojúhelníky v dolní řadě → 16 ((31 + 1) : 2 = 16).
Ze vzorce pro součet prvních n členů (16) aritmetické posloupnosti zjistíme celkový počet trojúhelníků.
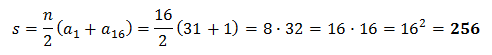
Správná odpověď je C.

Může se jednat o rovnoramenný nebo rovnostranný trojúhelník. Aby ortocentrum leželo vně trojúhelníku, musí se jednat o rovnoramenný tupoúhlý trojúhelník.

Správná odpověď je tedy D.


Správná odpověď je tedy B.

Vyjdeme z poznatku, že uhlopříčka ve čtverci je a√2.

Tím zjistíme velikost hrany krychle i výšky jehlanu. Objem je pak součtem obejmu krychle a objemu jehlanu.

Správná odpověď je tedy A.

Normálový vektor je kolmý na směrový vektor. Tím určime směrový vektor sq.
A dále podle zadání určíme směrový vektor sp.

Správná odpověď je E.
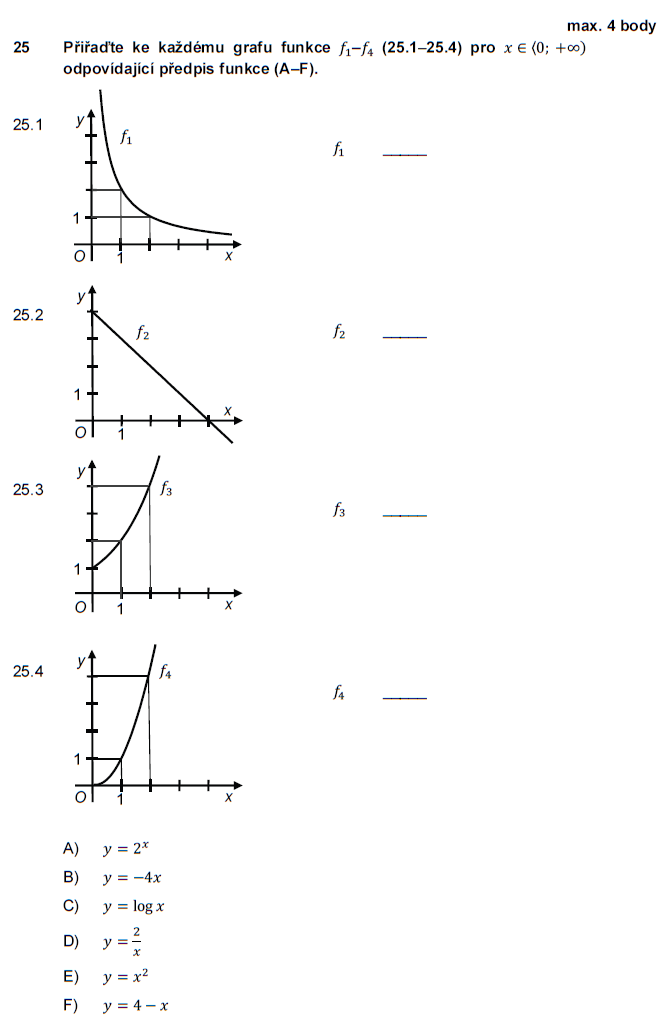
Podle tvaru grafu odhadneme, o jakou funkci se asi jedná, napíšeme si její obecný předpis a pomocí bodů, kterými dle zadání prochází, ověříme (dosazením souřadnic bodů), zda je to skutečně ona.

Odpovědi tedy postupně jsou D, F, A, E.

26.1
Pravděpodobnost, že ze skupiny devítí dětí, ve které jsou tři děvčata, bude jako první vylosována dívka je 3/9 = 1/3.
26.2

26.3

Odpovědi tedy postupně jsou B, A, E.
Zopakujte si, jak se počítá kombinační číslo…